What`s the Point?

Here`s the point :

"A point is a fundamental notion, which describes an absolute position in a defined space. It does not have any particular intrinsic meaning but is used as a reference within the context of a defined space. A point can be seen as a zero-dimensional entity".

Breaking down the above statements to understand the idea of a point in a defined space, we need to understand what is a defined space.

A defined space consists of various points and the arrangement between the points. And that defined space can be anything. We can consider the universe as the defined space, spanning in all directions indefinitely.

Imagine a string of beads.

Here, if we consider that each bead does not have any intrinsic property like shape, length, width... etc, i.e each bead is a point. As they are arranged in an order, each bead describes the absolute position(i.e order) of that particular bead in the context of the above-defined space. You can learn more about various notions of a point here and space here.

A point is zero-dimensional. But what exactly is a dimension?

Imagine a seesaw,

Here, if we observe the constraints in its movement, we can understand that one end of the seesaw can go up as long as the other end is going down and not touching the ground.

But within the constraints, one end can either go up or down and not any other way. So it is free to vary in one direction i.e up or down satisfying the constraints.

Now imagine a string with only a single bead.

Here, you can move the bead either left or right and not any other way. So it is free to vary in one direction i.e left or right.

"A dimension is something that adds a degree of freedom to the point in the defined space in some direction. Where the point can vary in that direction referencing a particular position along that direction."

If we consider the examples of a see-saw or a string with a single bead, the degree of freedom is 1, because it is free to vary in one direction within the given constraints.

But when our defined space is the whole universe, then we can consider the dimension to be infinitely indefinite in the direction in which that dimension exists without any constraints. And there can exist an infinite number of such dimensions, each adding a single degree of freedom.

What about a line?

"A line can be seen as an infinite set of points indefinitely in a direction. Which is nothing but a dimension. A line is one dimensional."

If we take the number line there is a number associated with each point. And let us say, we want to find how far (distant) two points(x1 and x2) are, then we can take the absolute difference between the numbers associated with each of the points. i.e distance = |x1 - x2|

A point on the number line can be moved left or right. Where it describes the position(i.e number) on the number line. Hence the degree of freedom is 1. Now let us add one more line exactly perpendicular to the existing number line.

Now the point can move left/right and up/down with reference to the dimensions x and y (Also referred to as x and y axis). Therefore, the degree of freedom in the above scenario is 2. And the point can be expressed as (x,y) which represents the position in the above-defined space. And this is called a (2D) two-dimensional space.

And if we want to find how far two points are in 2D space, then we can use the euclidean`s distance formula :

Now one may get a question about the formation of 2D space. "Why should the two lines be perpendicular i.e at an angle of 90 degrees to form the 2D space ?".

Well, one needs to understand that the whole business of dimensions is to put up a reference of measurement in the existing physical space around us and then identify the position of objects. And according to our current understanding, we are living in a 3-dimensional world. Where each dimension is perpendicular to the other two dimensions. Human perception is limited and can only perceive 3-dimensional and below 3-dimensional spaces. The system of having all the dimensions perfectly perpendicular to each other is called an orthonormal system. Which is commonly used in a lot of places. But there also exist other systems where it's not the case where all the dimensions need to be perfectly perpendicular to each other. We can learn about such systems by understanding basis vectors, and forward & backward transformations in tensor algebra. But for now, in the context of this article, we can stick to using an orthonormal system.

As you can see zero dimension is embedded within one-dimensional space. And one-dimensional space is embedded within two-dimensional space. Similarly, an n-dimensional space is embedded within n+1 dimensional space.

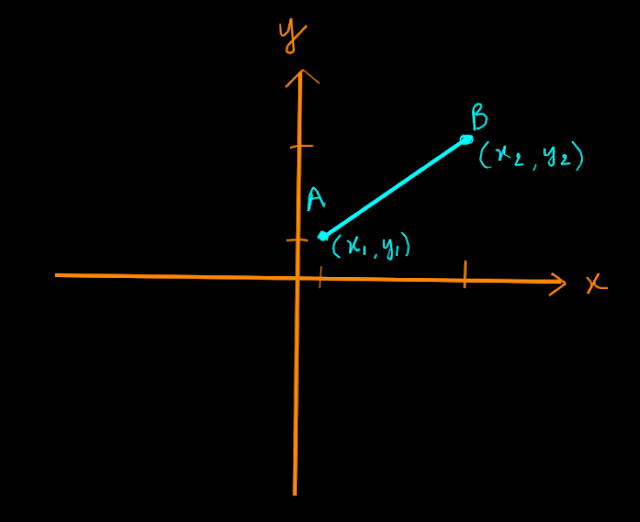
Now, Imagine two points A & B, and say we want to connect these two points, We can simply do that by drawing a line. But a line is nothing but a set of infinite points. And a line between two points is also called a line segment.

In a two-dimensional space, it looks something like this. The line segment AB can be seen as a directed line segment. Because it's in a certain direction. We will try to understand more about it when we get to the idea of the slope.

Although there can exist an infinite number of points between A and B. But to understand visually, we at least need a handful of points to connect A and B. And for that we can use the formula defined in Affine space here. I will explain why & how the formula works and about affine space in one of the next articles. The formula is :

Where λ is any value between 0 and 1. A and B are the points. Now let us take an example to understand how to calculate the points between A & B.

Now, the points can be calculated by varying the value of λ by adding it a value of 0.1, till the value of λ reaches 1. When the λ is 0, we get to point B, and when the value of λ is 1, we get the value of point A.

You can see this in the below graph :

One interesting that you can try out and see: What happens when λ value is not constrained between 0 and 1 but instead set to a greater value than 1 or a lesser value than 0.

Slippery Slope :

A line can be represented in slope-intercept form. You can read more about that here.

In simple words, this representation helps us build an infinite set of points (x,y) in a certain direction with the help of (slope) m. On the other hand, b decides where the line cuts the y-axis.

m controls the rotation of the line around the point where the line cuts the y-axis (also called y-intercept). So if we take the equation y = mx + 0 (i.e the line passes through the origin, making the b constant), and vary the value of m from -10 to +10, it would look something like the below.

And if we take the equation y = 2x + b, where m is constant and b is varied from -4 to +4, it would look something like the one below. Where the line is shifting up and down.

In the above examples although a line is one-dimensional, in two-dimensional space a line can be either rotated or shifted. i.e two degrees of freedom. But one needs to understand that those two degrees of freedom are not associated with the line, But with the dimensional space in which the line is embedded i.e two-dimensional space. As we have already discussed, a point is zero-dimensional, but in one-dimensional space, the point can be moved left or right (on the number line). And the degree of freedom (which is one in this case) is not a property of the point, but the property of the dimensional space in which the point is embedded.

So, every time you add a dimension, you are basically adding a degree of freedom to the point.

Imagine a car, and say our goal is to find how steep the road is on which the car is going. In other words, how hard it is for the car to move along the road.

When m=0, the line is perfectly parallel with the x-axis. And a car can go smoothly on such a road. But when m > 0, and the value of m is increasing in a positive direction, the line becomes steeper and steeper. Making it more and more hard for the car to move forward. And it is the same case when the value of m is decreasing in a negative direction. The only difference is, when m>0 the line`s inclination is from the bottom to the right direction, And when m<0 the inclination of the line is from the bottom to the left direction.

"Slope (m) is a number that explains the direction and steepness of any non-vertical line. The sign of the value of slope indicates the direction and the absolute value indicates the steepness."

Imagine a line that cuts the y-axis at point (o,b) and cuts the x-axis at point (x,y).

And if we want to calculate the slope we can take the ratio of rise over run i.e change in y to change in x. So we take a ratio of the distance of (y1,y2) to the distance of (x1,x2), then we would arrive at the slope-intercept form.

So if we have a line, we can take any two random points (x1,y1) and (x2,y2) and then calculate the slope using the below formula :

And the interesting thing here is that, for any two random points on the line, the value of the slope does not change. i.e for any non-vertical line the value of the slope is constant.

Then what would be the slope of a vertical line? undefined!.

If we imagine a curve like this :

The slope is not constant. And that is why we need calculus in the first place. We will discuss more on this in the upcoming articles. You can read about gradient, angle of inclination, and calculating slope using the angle of inclination here.